[알고리즘] 최소신장트리(MST)와 그래프의 순회(Graph Traversal)
신장 트리(Spanning Tree)
그래프 내의 모든 정점을 포함하는 트리
최소 연결 부분 그래프.
N개의 정점을 가지는 그래프의 최소 간선의 수는 N-1개이며, N-1개의 간선으로 연결되어 있으면 필연적으로 트리 형태가 이루어지고 이것이 바로 Spanning Tree라 할 수 있다.
하나의 그래프에는 많은 신장 트리가 존재할 수 있으며, 트리의 특수한 형태이므로 모든 정점들이 연결되어 있어야 하고 사이클을 포함해서는 안된다.
최소 신장트리(MST : Minimum Spanning Tree)
가능한 신장트리에서 간선의 가중치 합이 최소인 신장트리를 의미
최소 비용 신장 트리를 구하는 방법들은 모두 탐욕 알고리즘(Greedy Algorithm)으로 구현
** 탐욕 알고리즘 : 각 단계에서 최선의 선택이 최종 단계에서도 최선의 결과를 나타낼 것이라고 생각하는 알고리즘
크루스칼 알고리즘(Kruskal’s Algorithm)
간선 위주의 알고리즘.
- 모든 간선들의 가중치를 오름차순으로
정렬 - 가중치가
최소인 간선을 선택 - 위에서 선택한 간선이 연결하려는 2개의 노드가 서로 연결되지 않은 상태라면, 2개의 노드를 서로
연결(이 때, 사이클이 발생하지 않도록 주의) - 최소신장트리가 만들어지기 전까지 2~3 과정 반복 수행
그래프 내 간선의 개수가 적은 희소 그래프의 경우 크루스칼 알고리즘에 적합하다

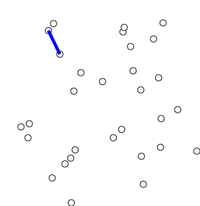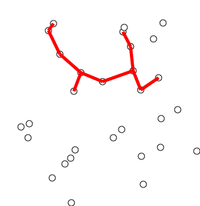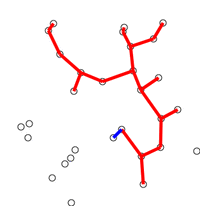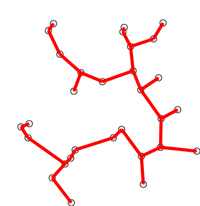
프림 알고리즘(Prim’s Algorithm)
정점 위주의 알고리즘
- 임의의
정점을 선택 - 정점에
인접한 간선 중 가중치가 최소인 간선으로연결된 정점을 선택 - 위 정점에서 다시 최소 간선으로 연결된 정점을 선택
- 최소신장트리가 만들어지기 전까지 2-3 과정 반복 수행
그래프 내 간선의 개수가 많은 밀집 그래프의 경우 프림 알고리즘이 적합하다
그래프의 순회(Graph Traversal)
하나의 정점에서 시작하여 그래프에 있는 모든 정점을 한번씩 방문하는 것을 그래프 순회 또는 탐색이라 한다
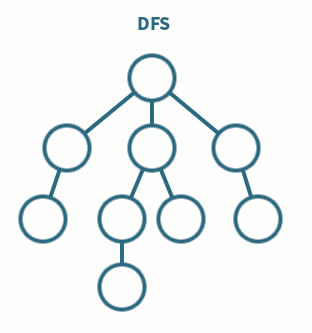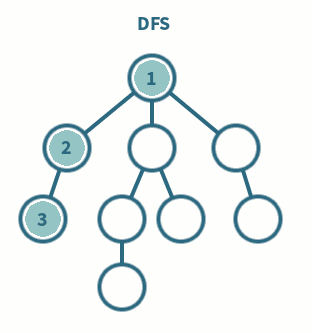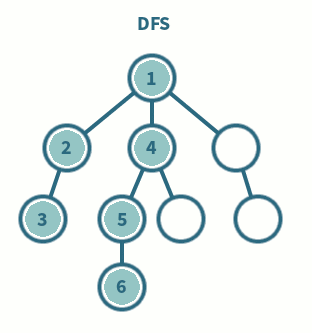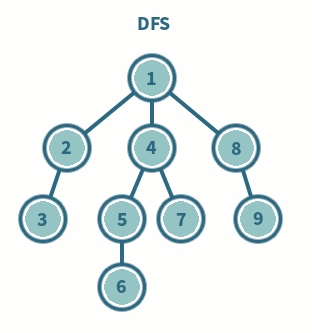
DFS(깊이 우선 탐색 : Depth-First Search)
아직 방문하지 않은 자식 노드를 우선적으로 탐색
- 정점 i를 방문한다.
- 정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면 이 정점을 모두
STACK에 저장한다 - 스택에서 정점을 삭제하여 새로운 i를 설정하고 다시 1단계부터 수행
- 스택이 공백이 되면 연산을 종료
- 특징
-
현 경로상의 노드만을 기억하면 되므로 저장 공간의 수요가 비교적 적지만, 한 경로가 무한히 깊을 경우 오버플로우가 발생할 수 있다.
이를 방지하기 위해, 깊이에제한을 두고 구현이 필요하다 -
목표에 도달하지 못할 가능성이 존재하며, 도달할지라도 해당 경로가 최단 경로라고 보장할 수 없다.
-
BFS(너비 우선 탐색 : Breadth-First Search)
형제 노드를 우선적으로 탐색하는 기법
- 임의의 시작 노드를 정해
QUEUE에 넣는다 - Dequeue연산을 통해 큐에서 노드를 가져와 현재 노드로 정한다
- 현재 노드의 인접 노드 목록을 순회하면서 방문하지 않은 노드가 있는지 확인한다
- 방문하지 않은 노드가 있다면 그 노드를 큐에 넣고 방문한다.
- 큐가 공백이 될 때까지 2~4과정을 반복 수행
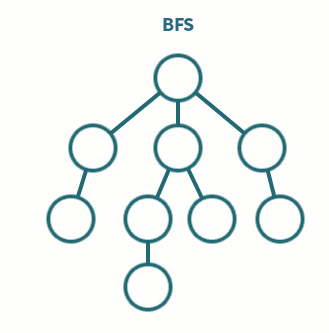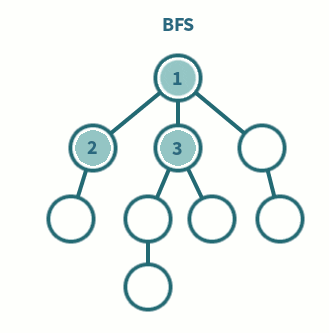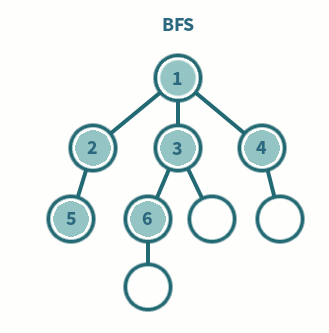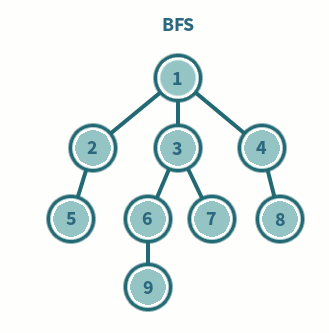
- 특징
- 큐에 다음에 탐색할 정점들을 저장해야 하므로 저장공간이 많이 필요
- 단순 검색속도가 DFS보다 빠르다
- 최단 경로를 보장함과 동시에 반드시 찾을 수 있다

댓글남기기