[데이터베이스] 관계 데이터 연산
관계 대수(Relational Algebra)
릴레이션으로부터 필요한 릴레이션을 만들어내는 연산자의 집합
주어진 릴레이션 조작을 위한 연산의 집합
원하는 정보와 그 정보를 어떻게 유도하는가(How)를 기술하는 절차적인 방법
관계 해석과 관계 대수는 표현 방법만 다를 뿐이지 표현 능력의 차이는 없다
집합연산자(Set Operations)
-
합집합(Union : ∪)
이항 연산으로 관계성이 있는 두 개의 릴레이션에 속하는 튜플의 집합을 구하여 하나의 릴레이션으로 만들어 내는 연산 -
교집합(Intersection : ∩)
이항 연산으로 관계성이 있는 두 개의 릴레이션에서 중복된 튜플을 선택하여 새로운 릴레이션을 만들어 내는 연산 -
차집합(Difference : -)
이항 연산으로 관계성이 있는 두 개의 릴레이션이 있을 때 그 중 하나의 릴레이션에서 또 다른 릴레이션의 튜플과 겹치는 튜플을 제거하여 새로운 릴레이션을 생성하는 연산 -
곱집합(Cartesian Product : ×)
이항 연산으로 두 개의 릴레이션이 있을 때 두 릴레이션의 튜플들을 접속하여 순서쌍의 집합을 만들어 새로운 릴레이션을 만들어 내는 연산결과 릴레이션의 차수는 연산 대상 릴레이션 차수를
더해서나오고 카디널리티는곱해서나온다
관계연산자(Relational Operations)
-
설렉션(Selection : σ(sigma))
단항 연산으로 릴레이션에서 조건에 맞는 레코드(튜플)을 분리해 내는 연산하나의 릴레이션에서 수평적 부분집합을 취하는 연산
A와 B를 릴레이션 R의 애트리뷰트,
θ는 비교 연산자(=,≠, <, ≤, >, ≥),
v는 상수라고 할 때σAθB(R) = {r t∈R ∧ r.Aθv} σAθB(R) = {r t∈R ∧ r.Aθr.B} 위와 같이 설렉션 연산을 표현한다
설렉션에 표현된 식 r.Aθv나 r.Aθr.B을 비교식/조건식/프레디킷(Predicate)이라 하는데 셀렉션은 바로 이 프레디킷을 참으로 만드는 튜플을 선택
-
프로젝션(Projection : ∏(pi))
단항 연산으로 릴레이션에서 구하고자 하는 속성을 선택하여 분리해 내는 연산하나의 릴레이션에서 수직적 부분집합을 취하는 연산
릴레이션 R이 있고, R에 속한 튜플을 t, A, B가 R 릴레이션의 속성이라 할때 프로젝션 여산의 수학적 표현은 다음과 같다
∏A, B(R) = {t.A, t.B t∈R} -
조인(Join : ⋈)
두 개 이상의 릴레이션에서 조건에 맞는 속성이 들어 있는 튜플을 접속하여 새로운 릴레이션을 생성하는 연산두 릴레이션 R과 K가 있다고 가정할 때
R에 속한 튜플을 r, K에 속한 튜플을 k,
R에 속한 속성을 A, K에 속한 속성을 B,
θ는 관계 연산자(=,≠, <, ≤, >, ≥)라 할 때 수학적 표현은 다음과 같다.R⋈AθBK = { r · k r∈R ∨ k∈K ∧ (r.Aθk.B) } -
세타 조인(Theta Join)
조인에 참여하는 두 릴레이션의 속성 값을 비교하여 조건을 만족하는 튜플을 반환 -
동등 조인(Equi Join)
세타조인에서=연산자를 사용한 조인을 의미R⋈R.C=K.EK
-
자연 조인(Natural Join)
동등 조인에서 중복된 속성을 제거한 결과를 반환R⋈NK
-
세미 조인(Semi Join)
자연조인을 한 후 두 릴레이션 중 한쪽 릴레이션의 결과만 반환닫힌쪽의 릴레이션 튜플만 반환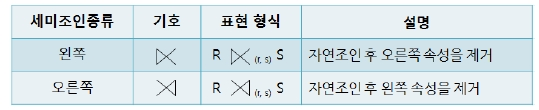
-
외부 조인(Outer Join)
자연 조인 시 조인에 실패한 튜플을 모두 보여주되 값이 없는 대응 속성에는 NULL 값을 채워서 반환종류 : 왼쪽 외부조인, 오른쪽 외부조인, 완전 외부조인
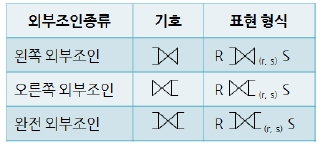
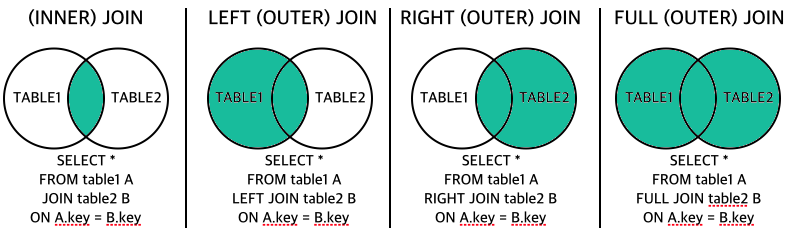
-
-
디비전(Division : ÷)
두 개의 릴레이션 R과 K가 있을 때 K 릴레이션의 모든 조건을 만족하는 경우의 튜플들을 릴레이션 R에서 분리해 내어 프로젝션하는 연산
관계 해석
수학의 프레디킷 해석(Predicate Calculus)에 기반
질의하는 형식으로 원하는 형태의 릴레이션을 정의하는 연산
구하고자 하는 정보가 무엇(What)이라는 것만 명시하는 비절차적 형태의 연산
관계 해석 기호
- ∀ : 모든 것에 대하여(for all)
- ∃ : 존재한다(There exist)
- ∈ : t가 r에 속함( t ∈ r )
- θ : 비교 또는 관계 연산자(=,≠, <, ≤, >, ≥)
- ∨ : OR 연산자
- ∧ : AND 연산자
- ㄱ : NOT 연산자
튜플 관계 해석(Tuple Relational Calculus)
원하는 릴레이션을 튜플 해석식으로 정의하는 표기법
- 정의
{t[A], t[B] | F(t)}
F(t) : 정형식 / t : 튜플변수 / t[A] : 한정 속성
도메인 관계 해석(Domain Relational Calculus)
원하는 릴레이션을 도메인 해석식으로 정의하는 표기법
- 정의
{ <x1,x2,…,xn>|F(x1,…, xn, xn+1,…, xn+m)}
<x1,x2,…,xn>: 구해야 할 도메인 변수
F(x1,…, xn,…) : 정형식의 구성 원칙에 따라 구성된 식

댓글남기기