[자료구조] 자료구조 기본
자료구조(Data Structure)
문제 해결에 있어 가장 효율적으로 자료를 조직하고 구조화하며, 자료를 표현하고 연산하는 일련의 활동을 의미한다.
자료구조의 분류
- 선형구조(Linear)
- 스택(Stack)
- 큐(Queue)
- 데크(Deque)
- 배열(Array)
- 연결리스트(Linked list)
- 비선형구조(Non-Linear)
- 트리(Tree)
- 그래프(Graph)
자료의 표현
- 외부 표현
- BCD 코드 : 6비트, 64가지 표현, 소문자는 표현 불가
- ASCII 코드 : 7비트, PC와 데이터 통신에서 주로 사용
- EBCDIC 코드 : 8비트, 대형 컴퓨터에서 주로 사용
- 내부 표현
- 수치 표현 : 컴퓨터 내부에 크기를 표현하기 위한 방법
- 포인터 표현 : 컴퓨터 내부에서 주소를 표현하기 위한 방법
- 논리 표현 : 긍정과 부정의 개념을 컴퓨터 내부에 표현하기 위한 방법
- 예외 표현 : 10진수 표현, 에러 검출, 데이터 송수신 등 용도로 사용
- 그레이 코드
- 3초과 코드
- 패리티 코드
- 해밍 코드
- 음수 표현 방식
컴퓨터 내의 연산 시 감산기(뺄셈)을 따로 만들지 않고 가산기(덧셈)만을 이용하여 덧셈과 뺄셈을 수행하기 위해 숫자자료는 보수 표현을 사용한다
- 부호화 절대치 : 첫 번째 비트가 0이면 양수이고 1이면 음수를 사용하는 방식
- 수의 표현 범위 : -(2n-1-1) ~ 2n-1-1
- 부호화된 1의 보수 : 양수의 1의 보수값을 음수로 사용
- 수의 표현 범위 : -(2n-1-1) ~ 2n-1-1
- 부호화된 2의 보수 : 양수의 2의 보수값을 음수로 사용
- 수의 표현 범위 : -(
2n-1) ~ 2n-1-1
- 수의 표현 범위 : -(
- 부호화 절대치 : 첫 번째 비트가 0이면 양수이고 1이면 음수를 사용하는 방식
선형 구조
데이터를 저장시키는데 있어 데이터와 데이터를 1:1 대응 구조로 관계 맺어 저장시키는 형태의 구조를 의미
스택(Stack)
처음 입력시킨 자료는 맨 마지막에 출력되고 맨 마지막에 입력시킨 자료는 맨 처음에 출력되는 LIFO(Last in First Out)구조
한쪽에서만 입출력하는 구조
- 스택의 응용 분야
- 함수 호출이나 서브 프로그램 호출 시 복귀를 지정할 때
- 인터럽트 분기 시 복귀 주소를 저장할 때
- 되부름 시 복귀 주소를 저장할 때
- 수식을 연산할 때
- 수식의 후위 표기법 변환
- 0주소 명령어 형식의 자료 저장소
삽입 알고리즘 (PUSH)
IF TOP >= M Overflow
TOP ← TOP + 1
STACK(TOP) ← X
TOP 포인터가 전체 크기 M보다 크거나 같으면 오버플로가 발생하고 그렇지 않으면 TOP 포인터 값을 하나 증가시켜 원하는 자료 X를 스택의 TOP포인터 위치에 삽입
삭제 알고리즘 (POP)
IF TOP = 0 Underflow
X ← STACK(TOP)
TOP ← Top - 1
TOP 포인터가 0과 같으면 스택에 데이터가 없는 것이므로 언더플로가 발생하고 그렇지 않으면 스택에서 TOP 포인터 위치와 값을 X에 넣어 삭제시켜주고 TOP 포인터 값을 하나 감소시킨다.
큐(QUEUE)
먼저 입력된 자료가 먼저 출력되는 FIFO(First In First Out) 구조 또는 FCFS(First Come First Serve) 구조라 불린다.
한쪽 방향에서는 입력만 하고, 다른 한쪽 방향에서는 출력만 이루어진다.
삽입(Rear or Tail)과 삭제(Front or Head) 포인터 두 개를 두고 운용한다.
삽입 시 Rear 값을 증가 시키고 삭제 시 Front를 감소시킨다.
- 큐의 응용 분야
- 스풀 운용 처리에 사용
- 운영체제의 스케줄링 작업에 사용
삽입 알고리즘(Enqueue)
IF rear >= M overflow
QUEUE(rear) ← X
rear ← rear + 1
Rear 포인터가 큐의 전체 크기 M보다 크거나 같으면 오버플로가 발생하고 그렇지 않으면 큐에서 Rear 포인터가 가리키는 위치에 X라는 자료를 삽입하고 삽입 포인터 Rear를 하나 증가시킨다.
삭제 알고리즘(Dequeue)
IF front = rear underflow
X ← QUEUE(front)
front ← front + 1
삭제 표인터 Front와 삽입 포인터 Rear가 같으면 데이터가 없는 언더플로가 발생하고 그렇지 않으면 큐에서 Front 포인터가 가리키는 위치의 값을 X에 치환하고 삭제 포인터 Front를 하나 증가시킨다.
데크(Deque)
포인터를 두 개 두고 운영(Left, Right)
양쪽끝에서 입출력이 일어나는 구조
입력 제한 데크는 스크롤(Scroll), 출력 제한 데크는 셀프(Shelf)
환형 큐(Circular Queue)
선형 큐는 front가 증가하여 Size 에 도달했을때 다시 빈 공간을 활용할 수 없다는 단점이 있는데,
이 점을 보완하여, 원형 큐를 사용하면 원형으로 배열 요소를 접근하게 하여 빈 공간에 다시 재할당이 가능해진다
큐가 가득 찬 경우와 큐가 비어있는 경우를 구분이 불가능한 단점
=> 배열을 가득 채우지 않고 배열의 길이 N일 경우 N-1개 채워졌을 때 이것을 가득 찬 것으로 가정하여 해결
환형 큐의 상태 알고리즘
// Empty
IF QUEUE → Rear == QUEUE → Front
EMPTY
// Full
IF (QUEUE → Rear + 1) % QUEUE_SIZE == QUEUE → Front
FULL
// EnQueue
IF FULL(QUEUE) Overflow
QUEUE → Rear = (QUEUE → Rear + 1) % QUEUE_SIZE
QUEUE → Data[QUEUE → Rear] = X
// DeQueue
IF EMPTY(QUEUE) Underflow
QUEUE → Front = (QUEUE → Front + 1) % QUEUE_SIZE
X = QUEUE → Data[QUEUE → Front]
배열(Array)
같은 크기의 기억 장소를 연속된 공간에 모아 놓고 원하는 데이터를 기록하거나 액세스하는 것을 의미
- 특징
엑세스 속도가 빠르다
삽입, 삭제가 어렵고 메모리에 종속적이다
연결리스트(Linked List)
자료를 구성할 때 포인터 자료를 포함해서 하나의 자료를 구성하는 형태로, 이 포인터를 이용해 현 자료와 관계있는 자료를 연결하는 형식으로 구성하여 저장
- 특징
액세스 속도가 느리다
중간에 단절되면 다음 노드를 찾기 어렵다
메모리에 대해 독립적이며 삽입, 삭제가 간편하다
메모리 단편화를 방지하여 기억 장소를 절약할 수 있다
포인터를 위한 추가 공간이 별도로 필요
비선형 구조
자료가 있을 때, 이 자료와 관계를 맺고 있는 다른 자료가 여러 개 존재하는 경우 이러한 관계성(1:N, N:M)을 표현하기 위한 구조
트리(Tree)
노드와 선분으로 되어 있고 정점 사이에 사이클이 형성되지 않으며, 자료 사이의 관계성이 계층 형식으로 나타나는 구조
여기서는 트리의 용어와 종류만 간단하게 언급하고 다음 장에서 부가 설명을 할 계획
- 용어
- 근노드(Root Node) : 트리의 뿌리가 되는 노드
- 단노드(Terminal Node, Leaf) : 노드의 차수가 0인 노드 또는 자식이 없는 노드를 의미
- 간노드(Nonterminal Node) : 노드의 차수가 0이 아닌 노드 또는 자식을 가지고 있는 노드를 의미
- 차수(Degree) : 각 노드의 가지 수, 또는 각 노드가 가지고 있는 자식 노드의 수를 의미
- 트리의 차수(Tree Degree) : 트리 전체에서 노드의 차수가 가장 큰 것을 의미
- 레벨(Level) : 근 노드를 1레벨로 하여 차례로 2, 3 레벨로 증가하여 표시
- 깊이(Depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야 하는 간선의 수
- 높이(Height) : 트리의 총 레벨을 의미
- 자노드(Child Node) : 각 노드에 연결되어 있는 다음 레벨의 노드를 의미
- 부노드(Parent Node) : 각 노드의 바로 상위 레벨에 있는 노드를 의미
- 제노드(Sibling Node) : 같은 부노드에 연결되어 있는 노드를 의미
- 숲(Forest) : 트리가 모여서 이루어진 집합
- 서브 트리(Sub Tree) : 임의의 노드를 제거했을 때 생길 수 있는 트리의 집합을 의미
- 트리의 운행(Tree Traversal)
- 중위 운행(Inorder Traversal) : <좌, 근, 우> 순서로 운행
- 전위 운행(Preorder Traversal) : <근, 좌, 우> 순서로 운행
- 후위 운행(Postorder Traversal) : <좌, 우, 근> 순서로 운행
- 레벨 순서 순회(Level-order Traversal) = 너비 우선 순회(Breadth-First Traversal) : 노드를 레벨 순서로 방문하는 순회 방법
- 위 3가지는 스택을 활용하여 구현이 가능하며, 레벨 순서 순회는 큐를 활용하여 구현이 가능하다
- 종류
- 이진 트리
- 이진 탐색 트리(AVL)
- 레드 블랙 트리
- 스레드 이진 트리
- B-트리, B+트리
- 이집 힙
그래프(Graph)
트리보다 더 일반적인 자료 구조이며, 그래프는 트리를 포함한다. 일반적으로 정점과 선분으로 되어있으면서 사이클이 형성되는 경우를 트리와 구별하여 그래프라 지칭
- 용어
- 그래프의 표시 : G = (V, E) {V: 정점들의 집합, E: 간선의 집합}
- 정점(Vertex) : 표현하고자 하는 대상 자료의 집합
- 간선(Edge) : 정점 사이에 관계
- 경로(Path) : 임의의 정점과 정점을 연결하는 경로
- 사이클(Cycle) : 경로의 길이가 2이상인 경로에서 종착점과 시작점이 같은 경로
- 차수(Degree) : 임의의 정점에 연결되어 있는 가지 수, 간선의 수
- 진입 차수(In-Degree) : 정점으로 들어오는 간선의 수
- 진출 차수(Out-Degree) : 정점에서 나가는 간선의 수
- 임의의 두 노드가 하나의 간선으로 연결돼 있을 경우, 이 노드들은 서로 인접(Adjacent)해 있으며, 간선은 두 노드에 부속(Incident)
그래프의 종류
-
비방향성 그래프(Undirected Graph)
간선 사이에 방향이 표시되지 않은 그래프. G(A, B)로 표현 -
방향성 그래프(Directed Graph)
간선 사이에 방향이 표시되어 있는 그래프. G<A, B>로 표현 -
완전 그래프(Complete Graph)
그래프를 구성한 모든 정점에서 자기 자신을 제외한 모든 정점에 대하여 간선이 있는 경우를 의미 -
레이블 그래프(Labeled Graph)
그래프에서 간선에 실수 레이블을 붙여 표시하는 그래프
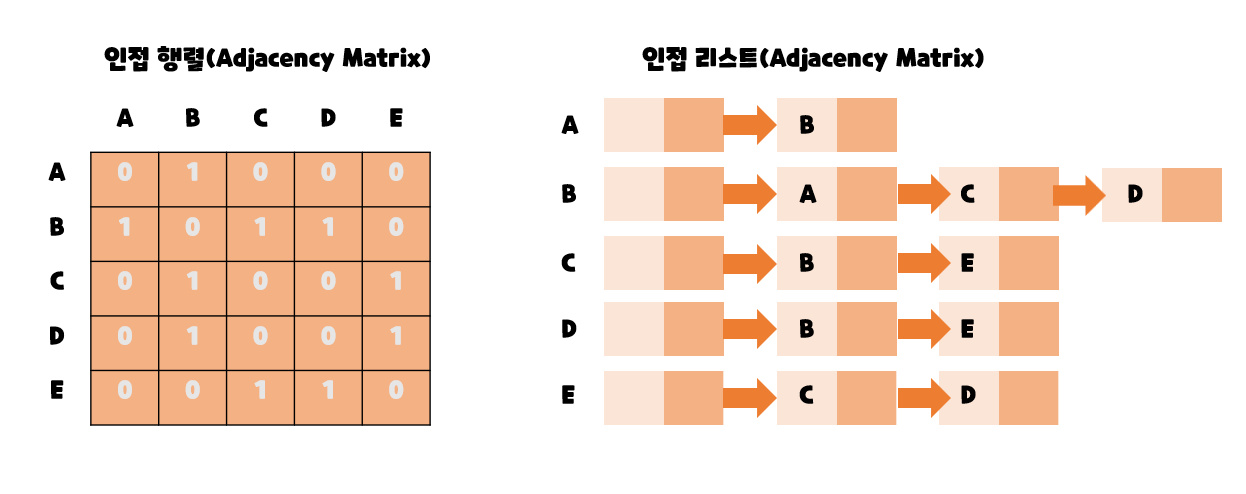
그래프의 표현
- 인접 행렬
- 인접 리스트

댓글남기기