[전자계산기] 자료 표현
자료 표현
사람과 컴퓨터 간에 의사소통을 위해서 인간이 사용하는 기호나 숫자 또는 문자 등을 컴퓨터가 인식할 수 있도록 표현하기 위한 기술을 의미
자료의 단위
| 단위 | 크기 | 설명 |
|---|---|---|
| 비트 | Bit | 0,1의 표현으로 전산기 구조의 최소 단위 |
| 니블 | Nibble | 4개의 비트를 묶어 하나의 단위로 나타낸 것으로 보통 16진수표현 단위로 사용 |
| 바이트 | Byte | 8개의 비트를 묶어 하나의 단위로 나타낸 것으로 문자 표현의 단위로 사용 |
| 워드 | Word | 내부 표현이나 처리를 위해 사용되는 단위 |
| 하프 워드 | Half Word | 2Byte |
| 풀 워드 | Full Word | 4Byte |
| 더블 워드 | Double Word | 8Byte |
| 필드 | Field | 어떤 특성이나 속성 표현을 위한 단위로 최소의 논리적 단위 |
| 레코드 | Record | 워드가 모여서 이루는 논리적인 단위로 정보가 처리되는 단위 |
| 블록 | Block | 입출력을 위해 논리 레코드를 묶어 놓은 단위로 물리적 레코드라고 한다 |
| 파일 | File | 관련있는 종류의 레코드를 묶어 나타낸 단위로 저장 장치에 저장되는 단위 |
| 데이터베이스 | Database | 서로 관련이 있는 파일을 통합하여 묶어놓은 데이터 그룹 |
문자 자료의 표현
-
표준 BCD Code
존(Zone) 2Bit와 디지트(Digit) 4비트의 총6비트로 하나의 문자를 나타낸다. 최대 64문자까지 표현 가능하며 초창기에 사용하던 코드영문자의 소문자는 표현이 불가능
-
EBCDIC Code
BCD 코드의 존 비트를 4비트 확장(총8비트)하여 최대 256문자까지 표현할 수 있도록 한 확장된 BCD 코드(Zone 4비트, Digit 4비트)IBM 사에서 개발한 것으로 대형 컴퓨터에 사용
-
ASCII Code(아스키코드)
7비트(Zone 3Bit, Digit 4Bit)로 한 문자를 표현할 수 있어 128문자까지 표현 가능하며 1비트의 패리티 비트를 합쳐 총8비트로 사용. 데이터 통신용으로 널리 사용되며, 특히 개인용 및 소형 컴퓨터용으로 쓰인다제어 부호 33개, 그래픽 기호 33개, 숫자 10개, 알파벳 대/소문자 52개로 구성
-
Unicode(유니코드)
컴퓨터에서 세계 각국의 언어를 통일된 방법으로 표현하도록 제안된 국제적인 문자 코드세계 26개 언어의 문자와 특수 기호에 대해 코드값으로 구성되어 있다. ASCII를 인식할 수 있지만, ASCII에서는 유니코드의 특수 문자를 인식할 수 없다
수치 자료의 표현
10진수 정수 표현
-
언팩 10진 형식(Unpack Decimal Format)
10진수 한 자리를 표현하기 위해 1바이트(8bit)를 사용하는 형식존 영역(4Bit) + 수치 영역(4Bit). 부호(+/-)는 마지막 존 영역에 표시(
+: 1100(C) /-: 1101(D))연산할 수 없으며 입출력을 위해 사용한다
-
팩 10진 형식(Pack Decimal Format)
연산이 가능하며 10진수 한 자리를 표현하기 위해 존 영역없이 4비트를 사용최하위 4비트에 부호를 표시(
+: 1100(C) /-: 1101(D))
2진수 정수 표현
- 부호와 절대치
최상위 1비트에 부호를 표시(+ : 0, - : 1)수의 표현 범위 : -(2n-1
-1) ~ 2n-1-10의 표현은 0000 0000, 1000 0000 2가지로 표현 가능
-
1의 보수
임의의 양수 값이 있다면 양수 값의 1의 보수 값을 그 값의 음수 값으로 사용하는 방식수의 표현 범위 : -(2n-1
-1) ~ 2n-1-10의 표현은 0000 0000, 1111 1111 2가지로 표현 가능
-
2의 보수
임의의 양수 값이 있다면 양수 값의 2의 보수 값을 그 값의 음수 값으로 사용하는 방식수의 표현 범위 : -(2n-1) ~ 2n-1-1
2진수 실수 표현
-
고정 소수점 표현 소수점이 항상 최상위 비트의 왼쪽에 고정되어 있는 방법
-
부동 소수점 표현 소수점위치를 변경시킴으로써 극히 작은 수에서 큰 수를 표현하는 방법
- 일반 부동 소수점 표현
- 부호(1) : 0(양수), 1(음수)
- 지수(7) : Bias 값 64에 지수값을 더해서 표현
- 가수(24) : 16진수로 표현
- IEEE754 표준 부동 소수점 표현
- 부호(1) : 0(양수), 1(음수)
- 지수(8) : Bias 값 127에 지수 값을 더해서 표현
- 가수(23) : 2진수로 표현
- 정규화
- 유효숫자를 늘려 정밀도를 높이기 위한 목적으로 사용
일반 정규형 : 0.M × 16E(단, M:가수, E:지수)
- 유효숫자를 늘려 정밀도를 높이기 위한 목적으로 사용
메가플롭스(MFLOPS) : 1초간에 실행되는 부동 소수점 연산의 수를 100만 단위로 하여 나타낸 수를 의미
- 일반 부동 소수점 표현
코드의 표현
| 분류 | 코드 종류 |
|---|---|
| 가중치 코드 Weighted Code |
8421코드 2421 코드 7421코드 8421 코드 5421코드 51111 코드 Biquinary 코드 Ring Counter 코드 |
| 비가중치 코드 Unweighted Code |
3초과 코드 그레이 코드 2-Out-of-5 코드 3-Out-of-5 코드 |
| 자기 보수 코드 Self Complement Code |
3초과 코드 2421 코드 5211 코드 51111 코드 8421 코드 |
| 에러 검출 코드 Error Detecting Code |
패리티 비트 코드 해밍 코드 Biquinary 코드 Ring Counter 코드 2-Out-of-5 코드 3-Out-of-5 코드 |
가중치 코드 : 2진수 각 자리마다 고유의 기준치 값이 있는 코드
자기 보수 코드 : 코드의 1의 보수가 10진수의 9의 보수가 같은 코드
8421 코드
- 4비트(8,4,2,1)의 가중 값을 가지므로 가중치 코드
- 2진화 10진수로 사용될 때는 10진수 0~9까지 표현
- 4비트 표현이므로 2진 표현으로는 16가지 표현이 가능하나 10~15까지는 사용하지 않는다
2421 코드
- 4비트(2,4,2,1)의 가중 값을 가지므로 가중치 코드
- 자기 보수 코드
- 4비트 표현이므로 2진 표현으로는 16가지 표현이 가능하나 그 중 2~7까지(6가지)는 중복 표현된다
7421 코드
- 4비트(7,4,-2,-1)의 가중 값을 가지므로 가중치 코드이며 가중치 값 중에 음수를 가지고 있다
허프만 코드(Huffman Code)
빈번히 발생하는 데이터의 코드는 적은 수의 비트로 표현하고, 빈번하지 않은 데이터는 상대적으로 많은 비트수로 표현하여 전체 데이터의 크기를 줄이는 방식
- 통계적인 부호화 방식
3초과 코드
- 비가중치 코드, 자기 보수 코드
- 8421 코드를 3초과시켜서 만든 코드
- 8421 코드는 뒤에서 6개의 코드 값을 사용하지 않지만 3초과 코드는 앞에서 3개, 뒤에서 3개를 사용하지 않는다
- 연산 시 캐리 발생 여부만 판별해서 3을 더해주거나 빼주면 되기 때문에 8421 코드에 비해 편리
그레이 코드(Gray Code)
- 각 자리에 일정한 값을 부여하는 가중치 값이 없는 비가중치 코드
- 한 비트의 변환만으로 다음 값을 만들 수 있기 때문에 변화가 적다
- 기계적인 동작을 제어하는 알맞은 코드이며, 입출력 장치의 동작이나 아날로그 신호를 디지털 신호로 변환하는데 사용할 수 있다
- 2진 코드 => 그레이 코드
- 2진 코드에서 최상위 비트(MSB: Most Significant Bit)는 변하지 않고 그대로 Gray Code로 변환
- 좌측 비트에서 오른쪽으로 이웃한 비트를 E-OR(Exclusive OR) 연산하여 차례로 그레이 코드의 다음 비트를 만들어 준다
- 그레이 코드 => 2진 코드
- 그레이 코드에서 최상위 비트(MSB)는 변하지 않고 그대로 Binary Code로 변환
- 변환된 2진 코드와 그레이 코드 오른쪽으로 이웃한 비트를 E-OR 연산 차례로 바이너리 코드의 다음 비트를 만들어 준다
해밍 코드(Hamming Code)포스트 이동하기
- 에러 검출뿐만 아닌 수정까지 가능한 코드
패리티 비트(Parity Bit)포스트 이동하기
- 2진수로 이루어진 코드에서 1의 개수가 홀수 개가 되는지 짝수 개가 되는지를 체크하기 위해 추가되는 비트를 의미
- 패리티 비트는 1비트 오류 검출이 가능

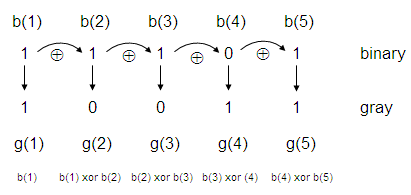
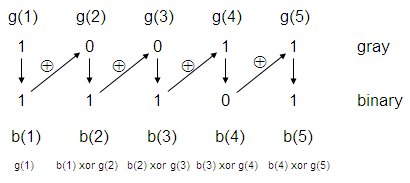
댓글남기기