[전자계산기] 논리 회로
불 대수
논리 회로를 분석하고 수학적으로 그 연산을 표현하고자 사용하는 대수식으로 논리 대수라고도 한다
- 논리 변수 사이의 진리표를 대수 형식으로 표시
- 논리 변수를 조작하여 주어진 회로 기능을 수행하는데 있어 가장 간단한 회로를 결정하고자 사용
- 불 대수의 모든 변수는 0과 1의 값을 가질 수 있다
- 논리 회로의 입출력 관계를 대수 형식으로 표시
- 불 대수의 연산
- 논리 부정(NOT,
 ̄또는') - 논리곱(AND,
·) - 논리합(OR,
+)
- 논리 부정(NOT,
| A + A = A | A · A = A | A · 0 = 0 | A + 0 = A |
| A + 1 = 1 | A · 1 = A | 0 + 0 = 0 | 0 · 0 = 0 |
| 1 + 0 = 1 | 1 · 0 = 0 | 1 + 1 = 1 | 1 · 1 = 1 |
| A + A·B = A | A·(A + B) = A |
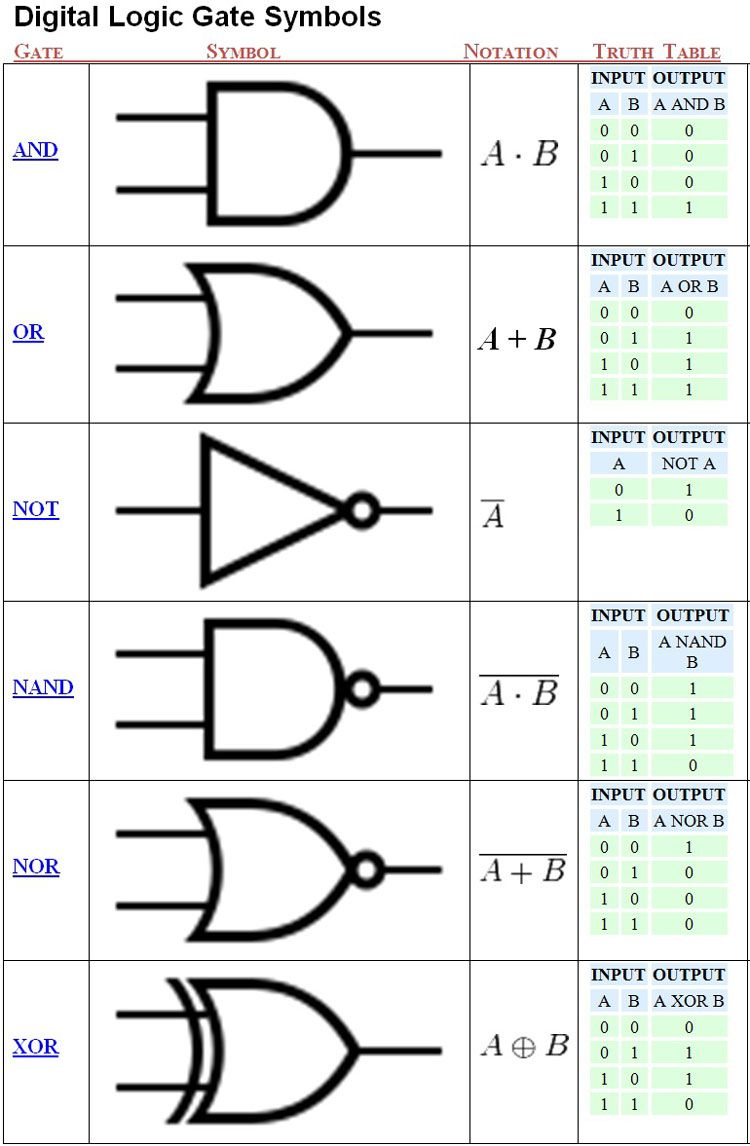
논리 게이트
논리 회로를 구성하는 기본 소자, 2진 정보를 취급하는 기본 논리 회로
| 이름 | 의미 |
|---|---|
| AND | 입력 값이 모두 1일 때만 1 출력 |
| OR | 입력 값이 모두 0일 때만 0 출력 |
| NOT | 입력 값이 0이면 1을 출력하고 1이면 0을 출력 |
| NAND | 입력 값이 모두 1일 때만 0 출력 |
| NOR | 입력 값이 모두 0일 때만 1 출력 |
| XOR | A, B 입력 값이 서로 다를 때는 1 출력, 같을 때는 0 출력 |
| XNOR | A, B 입력 값이 서로 같을 때는 1 출력, 같을 때는 1 출력 |
결선 게이트
필요할 때 게이트의 선을 연결하고, 단절하고 조절함으로써 다양한 기능을 할 수 있도록 만든 게이트를 의미
- 게이트들의 출력 단자를 논리적으로 직접 연결하여 논리 기능을 발휘할 수 있도록 했다
- 회로 비용을 절감할 수 있다
- 하나의 인쇄기판보다 많은 논리 기능을 포함시킬 수 있다
- Open Collector TTL(Transistor-Transistor Logic)로 게이트들의 출력 단자를 묶어서 사용한다
불 대수에 의한 최소화
-
최소항 : 진리표상에서 결과가
1인 부분을 표시할 때 사용하는 방식으로 불식을 형성하는 입력 변수 모두를 포함하는 논리곱(·)으로 나타내는 경우를 의미 -
최대항 : 진리표상에서 결과가
0인 부분을 표시할 때 사용하는 방식으로 불식을 형성하는 입력 변수 모두를 포함하는 논리합(+)으로 나타내는 경우를 의미
| A B | F | 최소항 | 수치 표현 |
|---|---|---|---|
| 0 0 | 1 | A · B | 0 |
| 0 1 | 0 | - | 1 |
| 1 0 | 1 | A · B | 2 |
| 1 1 | 1 | A · B | 3 |
최소항의 합 표현은 위 표에서와 같이 결과가 1이 되는 부분만을 논리곱으로 표현하여 이 논리곱들을 논리합으로 연결하면 된다
- 최소항의 합 : F = A · B + A · B + A · B
-
수치 표현 : F(A, B) = A · B + A · B + A · B = $\Sigma(0,2,3)$
- 불 대수식의 최소화
F = A · B + A · B + A · B
= B · (A + A) + A · B = B + A · B
= (B + A) · (B + B)
= B + A
| 입력(A, B, C) | 출력 | 최소항 | 수치 표현 |
|---|---|---|---|
| 0 0 0 | 1 | A · B · C | 0 |
| 0 0 1 | 0 | - | 1 |
| 0 1 0 | 1 | A · B · C | 2 |
| 0 1 1 | 0 | - | 3 |
| 1 0 0 | 1 | A · B · C | 4 |
| 1 0 1 | 0 | - | 5 |
| 1 1 0 | 1 | A · B · C | 6 |
| 1 1 1 | 0 | - | 7 |
- 최소항의 합 : Y = A·B·C + A·B·C + A·B·C + A·B·C
- 수치 표현 : Y(A, B, C) = $\Sigma(0, 2, 4, 6)$
- 불 대수식의 최소화
Y = A·B·C + A·B·C + A·B·C + A·B·C
= A·C·(B+B) + A·C·(B+B)
= A·C + A·C
= C

댓글남기기